An adaptive interconnected sliding mode observer based on battery electrochemical model for soc/soh estimation

Accurate estimation of the health of lithium-ion batteries will improve the performance and service life of electric vehicles, determine the actual degree of battery degradation during use and evaluate the available battery life after vehicle retirement, and reuse them for "secondary use" applications. Through electrochemistry, control theory and battery in the loop (bil) experiments, this paper verifies the real-time verification of an advanced battery health estimation algorithm. The algorithm is an adaptive interconnected sliding mode observer based on battery electrochemical model, which can simultaneously estimate key variables such as state of charge (SOC) and state of Health (soh). Bil experiment results show that in the face of incorrect initialization and sensor signal damage, the estimated soc/soh estimation converges to an error of 2% relative to its true value.

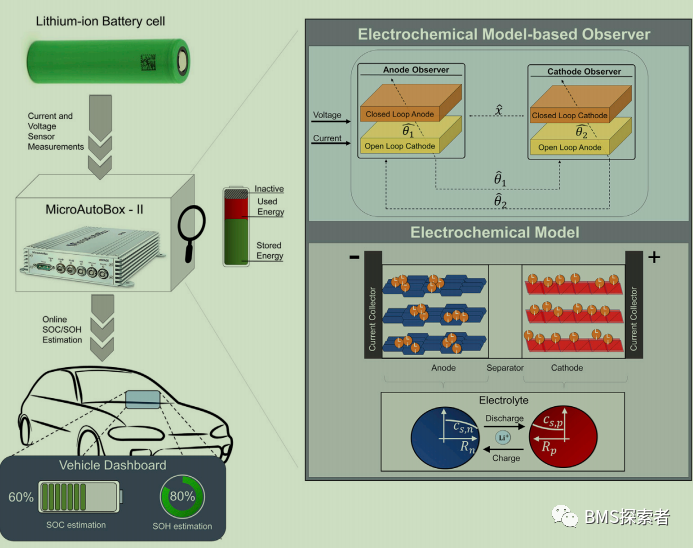
Battery in loop test

Replacing the hardware of the simulated battery model with a real physical system and a lithium-ion battery in this paper is called bil test. It can be seen that the code carried on the embedded controller is the code on the estimation algorithm. Bil is a more powerful verification method than HIL, in which the developed estimation algorithm can be tested in real time on the actual battery rather than its model. This test reduces development time and cost because it allows algorithms to be tested on hardware in the early stages of development. In addition, the test supports an iterative process to improve and correct the algorithm without spending time waiting for the HIL test phase. The main components of a bil are as follows, as shown in Figure 1:

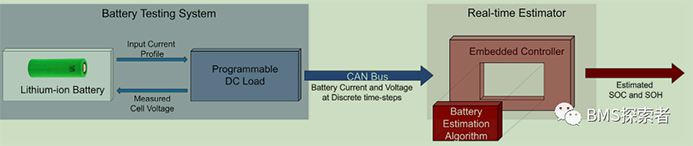
Electrochemical model

The electrochemical model of lithium-ion battery is characterized by a partial differential algebraic equation system, which describes the transfer of lithium in solid and electrolyte phases through the conservation laws of mass and charge. This model is usually called pseudo two-dimensional (P2D) model. It is a high-dimensional and high fidelity electrochemical model, which is traditionally used for battery design and modeling purposes. However, in this work, a low fidelity reduced order electrochemical model is derived from the P2D model, called the single particle model (SPM), which is used to give the observer on-line state / parameter estimation and minimize the computational effort, so that the model can run on the limited power capacity and resources of the real-time embedded controller. SPM assumes that each electrode can be extracted by a single spherical particle, as shown in Figure 2A. In addition, it is assumed that the current density of each electrode is uniform, and the dynamics of the electrolyte phase is ignored. These assumptions ensure that SPM has a lower computational burden than the full order model (P2D), but at the cost of accuracy.

Due to the neglect of electrolyte dynamics, the performance of the model at higher current magnification (c-rate=ibatt/qnom, where ibatt is the applied current and qnom is the nominal battery capacity) is inaccurate. SPM predicts the voltage behavior of the battery at the beginning of its life. However, with the aging of the battery, this expression will not reproduce the exact decay process of the cell. In this study, it is assumed that the growth of solid electrolyte interphase (SEI) layer is the main attenuation mechanism of lithium ion batteries. The relationship between capacity attenuation and power attenuation due to SEI layer growth is used to deduce that it can be incorporated into SPM. Therefore, considering that the voltage predicted by the battery aging SPM will accurately describe the performance of the battery declining with aging, for the real-time implementation of SPM, the partial differential equation describing lithium transport in the solid phase is spatially discretized by the finite difference method, and the ordinary differential equations (ODEs) of two electrodes are obtained.

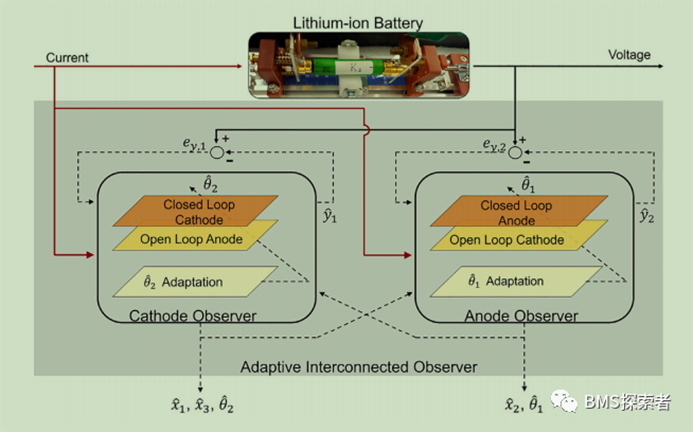
In this work, the idea of double observers is introduced to model, in which each electrode has a single electrode observer, which is hereby called cathode observer and anode observer. In the cathode observer, the lithium concentration in the cathode is estimated in a closed-loop manner, while the lithium concentration in the anode is estimated in an open-loop manner. Therefore, when estimating the cathode concentration state, the output error between the cathode observer output and the battery voltage measurement is considered. Similarly, the structure of the anode observer is similar, except that the lithium concentration in the anode is estimated in a closed-loop manner, while the lithium concentration in the cathode is estimated in an open-loop manner. Obviously, the open-loop models of these two observers are still prone to provide wrong values under incorrect initial conditions, which will lead to incorrect closed-loop estimation. This problem is solved by implementing two-way interconnection between two observers, which can correct the open-loop model over time. This bi-directional interconnection ensures that despite the initialization error of the concentration state in the two electrodes, the open-loop models in the two observers are updated and corrected, which ultimately ensures that the closed-loop estimates converge to their respective true values.

Bil test results

In order to prove the robustness of the observer, the model is incorrectly initialized to verify whether the model can converge to the true value in the case of initialization errors, sensor noise and damaged input signals. The variables estimated by the observer, i.e. SOC and battery capacity (soh), are compared with the true SOC value of the battery calculated using the Coulomb counting method and the true measured capacity of the battery (1.95ah), respectively In addition, the estimated variables obtained from these bil results are compared with mil test results by off-line simulation without computational constraints or input signal corruption. This comparison with the measured true reference value allows the user to evaluate the performance of the real-time validity of the estimate. The initialization error of lithium concentration (SOC) state is 15%, while that of capacity (soh) state is 7%. The cell is fully charged before using UDDS, while the SOC of the cell is 80% before applying wltp.

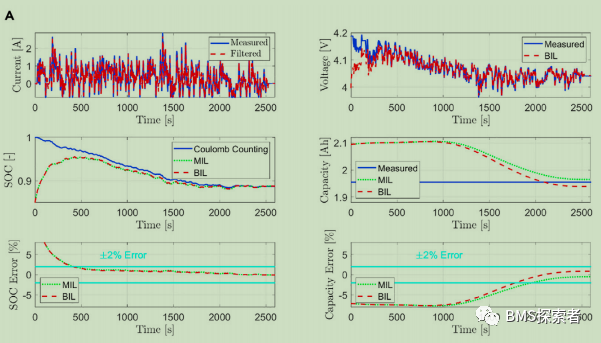
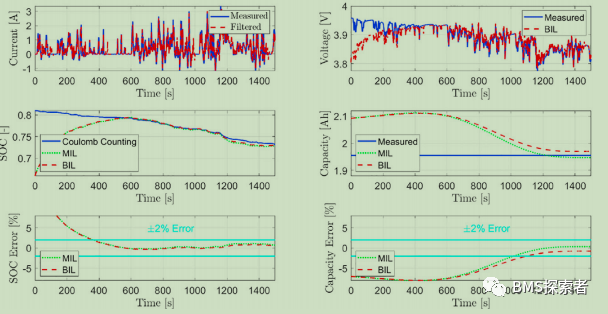
In the initial stage of the experiment, due to the initialization error of the observer, the initial SOC estimation error is high. The initial error of the cathode concentration state variable (constituent volume SOC) is 15% at the beginning to verify whether the observer can overcome this initial error error and still converge to the true value over time. As observed, although the input signal is corrupted, the bil estimate is comparable to the mil. The results further validate the actual stability concept, and show that the SOC and capacity estimates are always within the error range of 2% relative to the reference / measured values.

conclusion

In this paper, the limit of battery estimation algorithm is broken through the real-time realization of the real-time observer based on electrochemical model. The steps of establishing the communication between the physical lithium-ion battery and the embedded controller carrying the adaptive observer are summarized in detail. The SOC and SOH estimation results from bil are always within 2% of their respective true values, although the input signal is damaged in real time. The verification results show that an advanced estimation algorithm based on electrochemical model can run in real time, and can resist the noise and error caused by the real physical connection accurately. The feasibility of using this algorithm in real-time applications is to improve battery life, achieve accurate diagnosis / prognosis, and identify abnormal cells so that they can be used in "second use" applications after retirement.