Compared with the nonlinear Kalman filter, the two proportional integral filters can achieve accurate charge state with less computation and provide health state information for the battery management system. According to the error analysis of the equivalent circuit model of double resistance and capacitance, two proportional integral filters are used to compensate the inaccurate errors of charge state and current measurement. Combined with the recursive least square filter, the health status information can be provided, and the parameters of the battery model can be updated online to eliminate the error caused by parameter uncertainty. The method is compared with the extended Kalman filter in accuracy and execution time.
Two PI filters are used to compensate the error caused by inaccurate initial SOC and current measurement. However, according to the advantage of each PI filter to the modeling accuracy, the error between the battery model output and the terminal voltage is divided into two parts through the adaptive adjustment process. Then the output of PI filter is substituted into Coulomb counting function to estimate SOC. In order to obtain SOH information and avoid parameter uncertainty at the same time, RLS is used to identify the parameters of the two RC units online. Compared with EKF, the proposed model-based structure has better SOC estimation accuracy and lower computational complexity. The experimental results prove the effectiveness of these improved measures.
Error analysis of 2RC equivalent circuit
From this
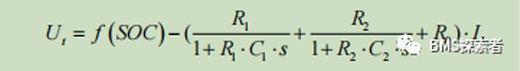
It can be seen from the formula that inaccurate SOC, current measurement error and RC parameter uncertainty will certainly bring errors to the model output. Because the initial SOC is not accurate, it is difficult to avoid errors in OCV. In addition, RC parameters change with the change of chemical reaction in the battery.
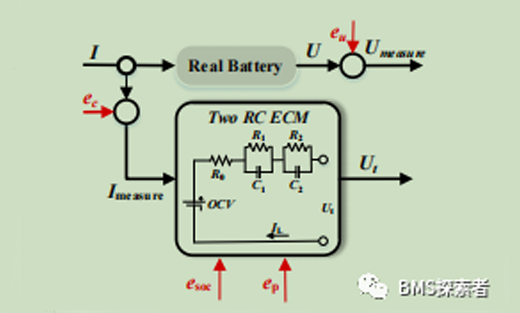
The inaccurate SOC error is defined as ESOC, the current sensor error is defined as EC, the voltage sensor error is defined as EU, and the parameter uncertainty error is defined as EP. The deviation between the output of the battery model and the voltage measurement serves as new information for correcting SOC in model-based estimation. δ U is defined as the difference between the output of the battery model and the terminal voltage. From the current measurement δ U is δ U1, from inaccurate SOC δ U is δ U2。 Parameter uncertainty δ The error of U3 is temporarily ignored, which will be discussed later in this article. Modeling error is expressed as:
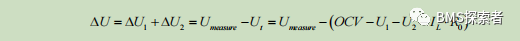
Design of two PI filters
The first PI filter is designed to eliminate current measurement errors δ U1。 Expression for first PI filter
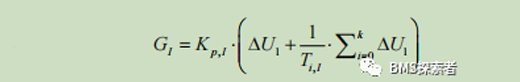
Battery model I ˆ The input current of is corrected by the gain of PI filter GI:
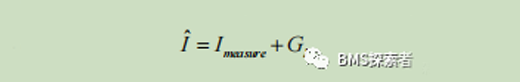
Then, I ˆ The feedback to Coulomb counting function is as follows:
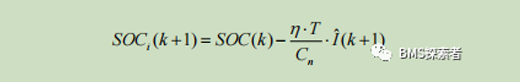
A second PI filter is established to reduce δ U2。 The expression for this PI filter is as follows:
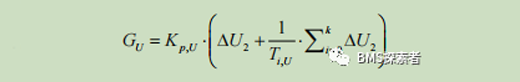
Due to the unique relationship between SOC and battery model output
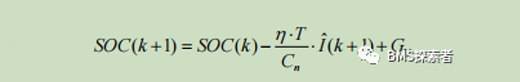
Considering that in most applications, it is difficult to know the accurate initial SOC in advance, at the beginning of the proposed method, the gain should be large, and then rapidly reduce after certain estimation steps. The updated coefficient is designed as the formula:
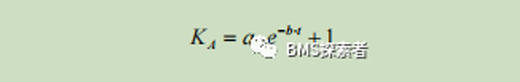
SOC estimation method is expressed as:
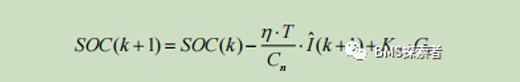
Framework of SOC estimation method
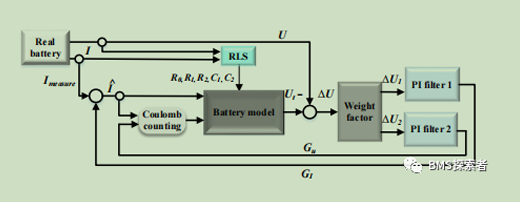
The adopted battery model is two RC ECMs that update parameters online through RLS parameter identification method. The difference between measured voltage and battery model output is divided into two parts: current measurement error and SOC estimation inaccuracy. Aiming at these two error sources, two PI filters are designed to improve the accuracy of the battery model. The outputs of the two PI filters compensate the estimated state of charge, which reduces the influence of the inaccurate state of charge and current measurement error in the traditional Coulomb counting method. Since PI filtering, ECM and RLS are effective methods for industrial applications, SOC can be estimated with low complexity. Section 4.2 will show the computational complexity of the proposed structure in more detail. Different from other structures with two PI filters, the voltage error is divided into two parts, as shown in the weight factor section in Figure 2. The objective of these two PI filters is to eliminate the errors associated with the current measurement and SOC uncertainties. Through this filter, the SOC of the battery can be estimated accurately. The error between the battery model and the voltage measurement is used to update the weight factor online.
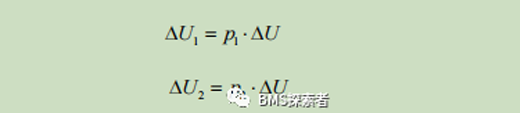
P1 and P2 are weight factors. Due to the nonlinearity of the internal characteristics of the battery, P1 and P2 are assigned to specify the initial values. Then, online updates are made throughout the estimation process to ensure the accuracy of SOC. The specific steps of the weight factor update mechanism are as follows:
Step 1: assumptions δ U is the input of the first PI filter to obtain the output of the battery model UA;
Step 2: assumptions δ U is the input of the second PI filter to obtain the output of battery type UB;
Step 3: the weight factor is calculated as follows:
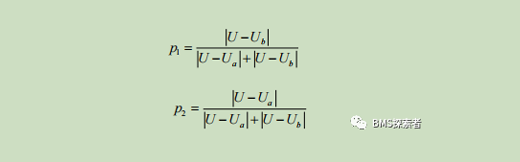
P1 and P2 actually fuse the results of the two PI filters. When SOC and current measurements are accurate, the output of the battery model shall be equal to the voltage measurement.
RLS online parameter identification
Transfer function of 2RC equivalent circuit:
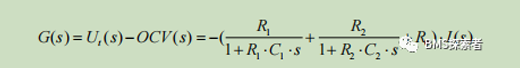
After discretization:
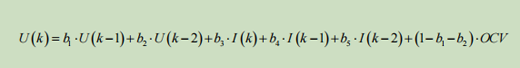
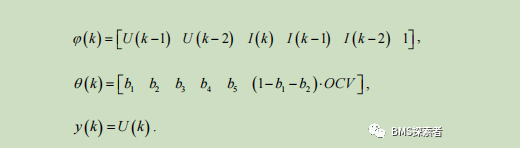
The equivalent circuit parameters are calculated by the following formula:
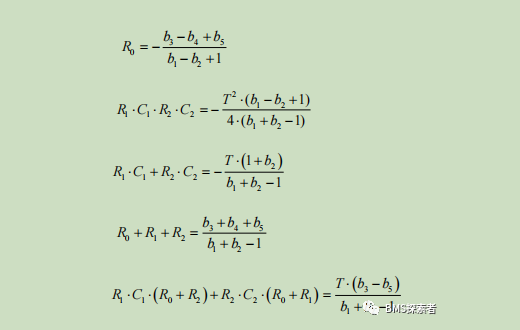





 Home
Home Products
Products Telephone
Telephone Message
Message






